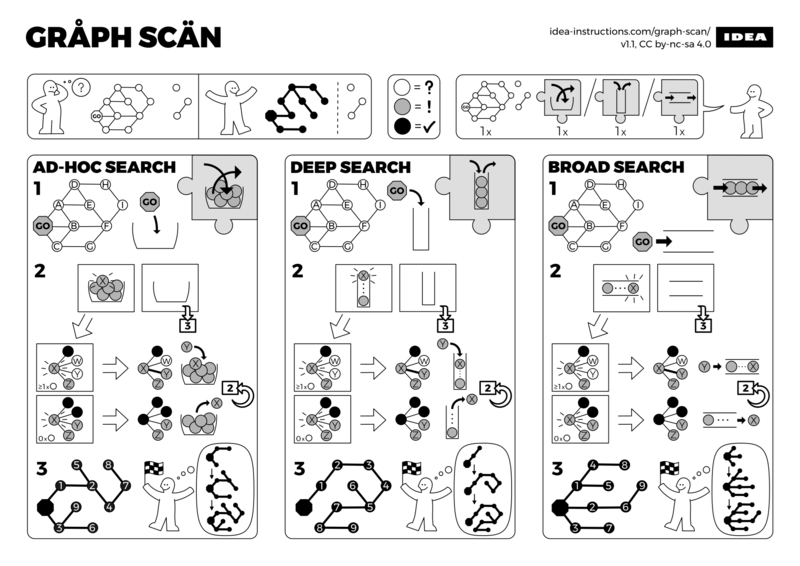
Depth-first search
A depth-first search (DFS) is an algorithm for traversing a finite graph. DFS visits the child vertices before visiting the sibling vertices; that is, it traverses the depth of any particular path before exploring its breadth. A stack (often the program’s call stack via recursion) is generally used when implementing the algorithm.
The algorithm begins with a chosen “root” vertex; it then iteratively transitions from the current vertex to an adjacent, unvisited vertex, until it can no longer find an unexplored vertex to transition to from its current location. The algorithm then backtracks along previously visited vertices, until it finds a vertex connected to yet more uncharted territory. It will then proceed down the new path as it had before, backtracking as it encounters dead-ends, and ending only when the algorithm has backtracked past the original “root” vertex from the very first step.
DFS is the basis for many graph-related algorithms, including topological sorts and planarity testing.

Breadth-first search
A breadth-first search (BFS) is another technique for traversing a finite graph. BFS visits the sibling vertices before visiting the child vertices, and a queue is used in the search process. This algorithm is often used to find the shortest path from one vertex to another.
